Figura 1: Linhas de
Campo Magnético produzidas por um condutor retilíneo percorrido por uma
corrente.
Considere um fio tal como da figura acima
percorrido por uma corrente estacionária.
Figura 2: Campo
magnético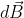
no ponto p devido a uma corrente .
Para calcular a indução magnética gerada pela corrente que
percorre o fio, considere um elemento infinitesimal do fio de comprimento dl. A lei de Bio-Savart mostra que a
indução magnética criada em um ponto p qualquer do espaço é:
Onde
é chamada de permeabilidade do vácuo (
T.m/A).
Integrando a equação
teremos:
A lei de Bio-Savart
permite obter o campo magnético para qualquer tipo de configuração de corrente,
desde que conhecida sua simetria angular.
Em exemplo, calcular o
campo magnético de um elemento de corrente. Primeiro acesse o Aplicativo:
Figura
3: Campo Magnético de um elemento de corrente
Na figura 3 temos o
campo magnético de um elemento de corrente. Neste aplicativo a posição do
observador com relação o elemento de corrente pode ser modificada de modo a ser
visualizada a mudança no valor do campo magnético.
Um fino e estreito fio
de corrente I é colocado ao longo do eixo x tal como na figura abaixo:
Figura
4: Fio estreito e fino carregando uma corrente I.
Para cálculo do campo
em um ponto P utilizaremos as equações anteriores da lei de Bio-Savart.
Considerar um elemento
diferencial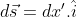
carregando uma corrente i na direção x. A localização é representado por
.
Sendo a localização do
ponto P em (x,y)=(0,a), a posição do vetor P é
.
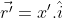O vetor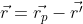
é um vetor de posição relativo. Sendo assim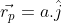e a sua magnitude
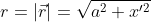é a distância entre a fonte e o ponto P. O
vetor unitário será:
O produto
será:
Para completar a
integral, reescrevemos r e x:
Substituindo:
Integrando a função de -θ1 a θ2, sendo θ1 negativo, pois leva em
consideração a porção do comprimento estendido a valores de x negativo.
Examinando os possíveis
valores de θ1e θ2:
Se θ2=-θ1, o ponto P está
localizado perpendicularmente ao plano bissetor. Se o comprimento da haste é 2L
então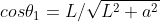
. O campo magnético
será:
Se L tende ao infinito, o limite será quando
(θ1,θ2)=(0,0), então o campo será:
Acesse o aplicativo:
Figura
4: exemplificação da lei de Bio-Savart
Considere um pequeno
fio de comprimento ds percorrido com corrente I. o vetor ds aponta na direção
da corrente. Vimos anteriormente que :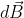
1)
É proporcional a 1/r²
2)
Proporcional a corrente i
3)
Proporcional ao comprimento do fio ds
4)
Proporcional a senθ, sendo θ o ângulo entre ds e r
No aplicativo verificar
as relações apresentadas modificando a posição dos pontos em rosa em torno da
representação do campo magnético para este ponto.
Outros aplicativos que
auxiliem a compreensão da lei:
Nenhum comentário:
Postar um comentário