Trata-se de um método alternativo para cálculo
do Campo Eletrostático gerado por uma distribuição de cargas. Utilizado sempre
com simetrias envolvidas. Evidencia a relação entre Carga Elétrica e Campo
Elétrico. O fluxo elétrico através de uma superfície fechada (gaussiana)
é proporcional à carga líquida que está envolvida pela superfície.
Onde qint
representa apenas a porção da carga que está envolvida pela superfície gaussiana
(S). εo = 8,85 x 10 -12 C2/N.m2: constante
de permissividade.
Caso mais simples: Verificar a lei de
Gauss para uma carga puntiforme q. Observações iniciais:
1)
De acordo
com o que vimos anteriormente, as linhas de força do campo gerado por uma carga
q são radiais com origem na
carga. Portanto, se escolhermos uma superfície esférica de raio r (distância da carga ao ponto onde
queremos calcular o campo), a normal a esta superfície terá também direção
radial em qualquer ponto;
2)
Elemento de área é :
sendo dA o elemento de área de uma esfera.
Sendo esta a
expressão para Lei de Coulomb envolvendo duas cargas q e q0. A densidade
de cargas serão conforme as equações abaixo:
Densidade de
carga volumétrica:
Densidade de carga Superficial:
Densidade de carga Linear:
Em
alguns casos é necessário adicionar algo que auxilie na resolução, neste caso,
com argumentos de simetria teremos ideia de como o campo aparece.
O fluxo elétrico para qualquer
superfície fechado é igual á carga resultante encerrada na superfície, dividido
por εo.
O fluxo elétrico depende do campo
elétrico, ou seja, a lei de Gauss estabelece uma maneira de relacionar o campo
elétrico em torno de uma dada região (superfície) com a distribuição de cargas
que o produz.
Aplicações
da Lei de Gauss
Figura 1: aplicações da
Lei de Gauss para carga pontual, cilindro carregado, esfera, múltiplas cargas e
placas carregadas em paralelo.
Podemos
utilizar a Lei de Gauss para calcular o campo elétrico produzido por
distribuições contínuas de carga, quando as mesmas exibirem algum tipo de
simetria.
1º. Caso: Simetria Cilíndrica
Campo
elétrico de um fio infinito e a superfície gaussiana é um cilindro de raio r e
altura h
Figura 2:
Cálculo do campo para um fio infinito
Considerações de simetria:
(i) o campo elétrico tem
direção radial, ou seja, é perpendicular a todos os pontos da lateral da
gaussiana cilíndrica;
(ii) o campo elétrico tem o
mesmo módulo em todos os pontos da lateral da gaussiana.
Usando a consideração (i), o
campo tem direção radial
Base 1: como o campo é
perpendicular ao elemento de área, θ = 90o, cos 90o = 0,
Base 2: novamente campo é
perpendicular ao elemento de área, θ = 90o, cos 90o = 0,
Lateral: como campo é paralelo à
área, θ = 0o, cos 0o = 1,
Usando a consideração (ii) o campo elétrico é
constante ao longo da lateral
Pois a área da superfície lateral
do cilindro (retângulo) é o comprimento da base (2πr) multiplicado pela altura
h.
Carga envolvida
pela gaussiana: como a barra está uniformemente carregada, a gaussiana cilíndrica tem comprimento h e
densidade linear de carga.
Lei de
Gauss:
O campo elétrico gerado pela
barra cai com o inverso da distância (não
é uniforme). As linhas de força têm direções radiais a partir da barra. Se a
carga da barra é positiva, as linhas apontam para fora da barra, caso contrário
(carga negativa), apontam para dentro.
2º. Caso: Simetria Plana
Campo
Elétrico de uma Plano Infinito de Cargas: placa plana fina e
infinitamente extensa, com uma carga distribuída uniformemente sobre sua
superfície. A superfície gaussiana S é um cilindro que de raio da base r e
altura 2r que intercepta a placa perpendicularmente.
Figura 3:
Cálculo do campo de um plano infinito de cargas
Considerações
de simetria:
(i) E é
perpendicular à placa, em particular é perpendicular às bases do cilindro;
(ii) E é
constante para todos os pontos a uma mesma distância r da placa, ou seja,
constante para as bases do cilindro;
(iii) E
aponta para fora dos dois lados da placa, se esta for positivamente carregado,
e para dentro dos dois lados da placa se esta for negativamente carregada.
Usando a
consideração (i) campo elétrico é sempre perpendicular à placa
Base 1:
como o campo é
paralelo ao elemento de área, θ = 0o, cos 0o
= 1,
Base 2:
novamente campo é paralelo a dA, θ = 0o,
Lateral: Campo é perpendicular a dA, θ = 90o, cos 90o
= 0,
Usando a
consideração (ii) o campo é constante ao longo da lateral
Carga
envolvida pela gaussiana: carga de um círculo de área A. Obs. Nem precisamos
escrever A = π r2, pois a área é simplificada no cálculo. Densidade
superficial de carga.
Lei de
Gauss:
O campo
elétrico de um plano infinito é uniforme: não depende da distância r ao
plano, e as linhas de força são paralelas entre si e perpendiculares ao plano
de cargas
Figura 4:
esquema das linhas de força paralelas e perpendiculares em relação ao plano
Se o
plano está positivamente carregado, as linhas de campo afastam-se do plano em
ambos os lados. Se o plano está negativamente carregado, as linhas convergem
para o plano também em ambos os lados.
Em geral,
o campo elétrico nas proximidades de QUALQUER superfície condutora é
perpendicular à superfície e tem módulo:
A
demonstração segue essencialmente os mesmos passos da que foi apresentada para
a simetria plana, pois vale para a região imediatamente próxima de qualquer
ponto da superfície do condutor, independentemente da forma deste. Em
particular, o campo elétrico produzido por um plano infinito condutor não é σ/2εo, e sim
σ/εo, em conformidade com o resultado anterior.
Condutor isolado num campo elétrico externo: Dentro
do condutor vimos na aula passada que E = 0. As linhas de força no exterior do
condutor são tais que interceptam perpendicularmente a superfície do condutor.
O módulo do campo é proporcional à densidade superficial de carga no condutor.
Quanto maior a densidade de linhas de força que entram ou saem do condutor numa
certa região, maior a carga superficial nesta região.
3º. Caso: Simetria Esférica
Campo
elétrico gerado por uma casca esférica de raio R
Acesse o
Aplicativo:
Figura 4:
Simulação carga positiva envolta por uma superfície gaussiana esférica.
1) para
pontos fora da casca (isto é, a distâncias radiais r > R): superfície
gaussiana S é uma esfera de raio r envolvendo a casca. Como as linhas de força
apontam radialmente para fora, o campo elétrico em todos os pontos da esfera é
paralelo ao elemento de área vetorial dA. Logo
Em todos os pontos da esfera o
campo elétrico tem o mesmo módulo (simetria esférica), logo o campo é constante
enquanto integramos sobre a superfície S de área A = 4πr2. O fluxo
elétrico pela superfície esférica S será:
Pela lei
de Gauss:
Isolando o campo E
Ou seja, o campo elétrico para
pontos fora da casca é o mesmo que seria obtido se toda a carga da casca
estivesse concentrada em seu centro.
2) para
pontos dentro da casca (isto é, a distâncias radiais r < R): o fluxo
elétrico é o mesmo do caso anterior, pois a gaussiana é novamente uma esfera de
raio r (só que dentro da casca)
Pela lei
de Gauss:
Como q =
0 dentro da casca, Campo Elétrico=0 .
|
|
Vejamos o
seguinte aplicativo:
Figura 5:
Aplicativo para visualização das superfícies esféricas.
Nele é
possível observar os diferentes tipos de carga e as linhas de campo
resultantes. Também é possível aumentar a força do campo e densidade de linhas.






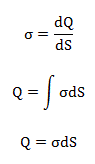






















Nenhum comentário:
Postar um comentário