Teorema de Stokes

    O Teorema de Stokes diz que a integral dupla do rotacional de um campo vetorial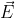na superfície aberta S definida pela curva fechada C é a integral de linha de  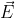na curva C:

    Para mostrar o teorema de Stokes, imagine a superfície arbitrária subdividida em circuitos infinitesimais, como na figura abaixo. A integral na superfície é obtida somando as contribuições dos vários circuitos quadrados, cada uma dada pela equação abaixo:

Figura 1:Superfície arbitrária é preenchida por circuitos quadrados infinitesimais

    Na soma das circulações dos quadrados, as contribuições de lados internos se cancelam, pois vem sempre em pares de sinais opostos. Sobra apenas a contribuição da curva externa delimitando a superfície:

    Note que todos esses casos correspondem esquematicamente a:

    Ondedenota derivadas generalizadas (em 1, 2 ou 3 dimensões),denota um campo generalizado (escalar ou vetorial), A denota uma região generalizada (intervalo, superfície ou volume) e ∂A denota a fronteira de A (ponto, curva ou superfície).